摘要：探讨了隐含波动率排名（IVR）和隐含波动率百分位（IVP）的概念及其计算方法。IVR 和 IVP 用于评估当前隐含波动率相对于历史水平的高低，帮助交易者判断期权的价格是否便宜或昂贵。通过对比历史数据，这两个指标为交易者提供了重要的市场背景信息。

隐含波动率排名（IVR）和隐含波动率百分位（IVP）这两个统计指标都衡量当前隐含波动率（IV）与历史 IV 值范围的比较。可以计算任何时间段的这些统计数据，但通常使用过去一年的值范围。

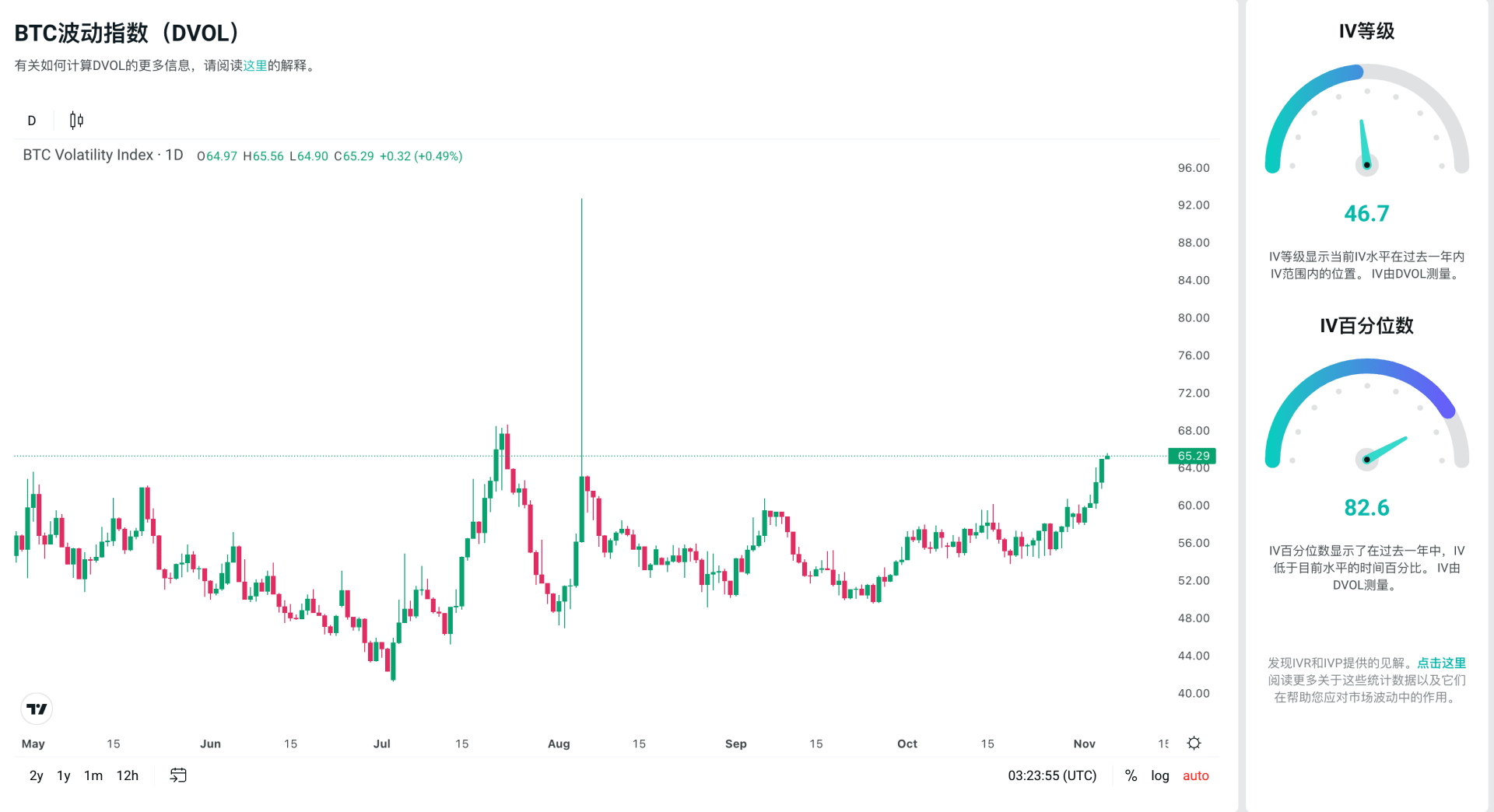
IVR 将当前 IV 与过去一年的历史 IV 范围进行排名，而 IVP 则显示过去一年中 IV 低于当前水平的时间百分比。

这两个指标的值范围在 0 到 100 之间。对于 IVR 和 IVP，值为 0 表示 IV 相对于正常水平非常低，而值为 100 则表示 IV 相对于正常水平非常高。这里的“正常”仅指过去一年的值范围。

由于 IV 告诉我们期权的便宜或昂贵程度，因此 IVR 和 IVP 可以用来评估当前期权的便宜或昂贵程度，相对于每个基础资产的特定值。

IVR 和 IVP 为 IV 提供对比的上下文背景

IV 允许不同期权之间进行更好的价格比较，因为它考虑了影响期权价值的因素，如时间和内在价值。这使得每个期权价格可以表示为年化波动率。

IVR 和 IVP 通过允许与基础资产的历史标准进行更好的比较，进一步提供了背景。

如果比特币的 IV 为 45%，这算高还是低？对于像标准普尔 500 这样的美国股票指数，45% 的 IV 算高，但对于 2021 年在零售期权交易者中流行的“迷因股票”如 GameStop 或 AMC 来说，这算低。我们需要为 IV 值提供一些上下文背景。

IVR 和 IVP 通过将当前资产的 IV 与该资产的历史 IV 值进行比较，给我们提供了这种背景。每个统计指标将这种比较简化为 0 到 100 之间的单一值，每个值传达的信息略有不同。

计算方法

将使用 DVOL 指数数据。

IVR 告诉我们当前 IV 在历史 IV 范围内的位置，计算公式为：

(当前 IV – IV 最低值) / (IV 最高值 – IV 最低值) * 100

其中：

• 当前 IV = 当前的隐含波动率。
• IV 最低值 = 在过去一年中基础资产的最低隐含波动率。
• IV 最高值 = 在过去一年中基础资产的最高隐含波动率。

（所有数据均由 DVOL 测量）

IVP 告诉我们 IV 低于当前 IV 值的时间百分比，计算公式为：

低于当前值的周期数 / 总周期数 * 100

其中：

• 低于当前值的周期数 = 在过去一年中隐含波动率低于当前水平的周期数。
• 总周期数 = 在过去一年中的总周期数。例如，如果周期为 1 天，则总周期数为 365。

计算这两个统计数据所需的唯一数据是过去一年的 DVOL 指数历史数据。

为什么同时显示 IVR 和 IVP？

这两个统计数据展示了相同事物的不同版本，因为它们都显示当前 IV 与过去一年 IV 的比较。然而，由于它们在某些数据上的表现差异，查看这两个指标仍然是有用的。

IVR 对异常值更敏感。单个极高的 IV 值可能导致 IVR 在很长一段时间内保持相对较低的值，直到该单一数据点从比较周期（通常为一年）中消失。IVP 则不会受到此影响，因为它不查看所有值的范围，而仅测量低于当前 IV 水平的时间，因此单日的 IV 值仅占 IVP 值的 1/365。

然而，IVP 可能对 IV 的小变化过于敏感，这取决于当前 IV 相对于先前值的分布。而 IVR 则更一致地处理 IV 的变化规模。IV 的小变化通常意味着 IVR 的小变化。

IVR 和 IVP 可能的差异示例

假设当前 IV 为 60，我们有以下 10 个历史 IV 读数：

[100, 50, 70, 59, 50, 50, 50, 50, 50, 50]

在这种情况下，IVR 的读数为 20，因为 60 的值在 50 到 100 的范围内占 20%。

(当前 IV – IV 最低值) / (IV 最高值 – IV 最低值) * 100
= (60 – 50) / (100 – 50) * 100
= 20

这使得 IV 看起来相对较低。然而，当前的 60 值高于大多数先前的读数。

让我们看看 IVP 是否提供更多信息。IVP 的计算为：

低于当前值的周期数 / 总周期数 * 100
= 8 / 10 * 100 = 80

IVP 在这里给出了非常不同的印象。它告诉我们，IV 在 80% 的时间里低于当前的 60 值。

这两个统计数据结合在一起告诉我们，尽管 IV 在某些时候远高于当前的 60 水平，但它在大多数时间（80%）内低于该水平。

通常，这两个统计数据不会像这个例子中那样相差甚远，通常会传达类似的故事。例如，如果它们都超过 90，我们可以确信 IV 高于正常水平。如果它们都低于 10，我们可以确信 IV 低于正常水平。然而，如果它们出现分歧，我们可以查看 DVOL 图表以了解原因。

继续这个例子

假设我们向前移动一个时间周期。我们仍然只使用之前的 10 个读数进行比较，因此我们的历史值现在是：

[50, 70, 59, 50, 50, 50, 50, 50, 50, 60]

请注意，之前的最高值 100 已从数据集中删除。

假设我们当前的 IV 读数为 61。这比之前的 60 高出一个点，因此 IV 几乎没有变化。这对 IVR 和 IVP 的读数有何影响？

IVR = (61 – 50) / (70 – 50) * 100 = 55
IVP = = 9 / 10 * 100 = 90

IVR 从 20 变为 55，IVP 从 80 变为 90。IV 从 60 略微增加到 61，因此看到这两个统计数据增加并不奇怪。然而，我们现在可以看到，掉出数据集的一个数据点对 IVR 的影响是多么显著。范围从 50-100 变为 50-70。因此，尽管 IV 略微增加，IVR 却大幅上升，而 IVP 的增加幅度则小得多。

最后，假设我们再向前移动一个时间周期，因此我们的历史值现在是：

[70, 59, 50, 50, 50, 50, 50, 50, 60, 61]

假设我们当前的 IV 读数现在为 58。这比之前的 61 低了 3 点。这对 IVR 和 IVP 的读数有何影响？

IVR = (58 – 50) / (70 -50) * 100 = 40
IVP = = 6 / 10 * 100 = 60

IV 减少，因此看到这两个值下降并不奇怪。IVR 从 55 降至 40（减少 15），但 IVP 从 90 降至 60（减少 30）。IVP 的这种变化似乎夸大了 IV 仅变化 3 点的相对小幅度。这是因为越来越多的数据点接近当前 IV 水平。因此，当当前 IV 在这些值的聚集区间两侧移动时，成为高于或低于当前水平的值的百分比会更大。

通过这个例子，我们已经涵盖了如何计算每个统计数据，以及哪些情况可能导致每个统计数据的过度变化。我们看到，IVR 可能仅因一个极端数据点的消失而发生剧烈变化。我们还看到，IVP 即使在 IV 仅变化相对较小的情况下也可能发生剧烈变化。这种情况发生在许多先前的数据点聚集在当前 IV 附近时。

虽然波动率在长期内是均值回归的，但它在短期内往往会聚集。这意味着它可以在短期内维持极端值。仅仅因为 IV 非常低，IVR 和 IVP 都显示低于 5 的值，并不意味着 IV 不会在接下来的几周甚至几个月内继续保持低位。

同样值得注意的是，即使 IVR 和 IVP 都处于最大值 100，这并不意味着波动率不能进一步增加。100 的读数仅表示 IV 在测量周期（通常为 1 年）内是最高的。然而，它仍然可以进一步增加，设定新的历史最高点，并保持 IVR 和 IVP 值固定在 100，直到 IV 最终从新高回落。

同样，当 IVR 和 IVP 都处于最小值 0 时，波动率仍然可以进一步下降。

尽管极端读数可能倾向于均值回归，但并没有保证一定会发生。