Amberdata 期权 PDF 和 CDF 图表使用介绍

专栏: 加密货币期权 · · 2025年01月12日 · 7 次阅读

PDF probability density function

PDF probability density function 翻译为：概率密度函数，可以用来观测不同到期日行权价对应的密度，值越大表示到期时在该行权价的概率越高。

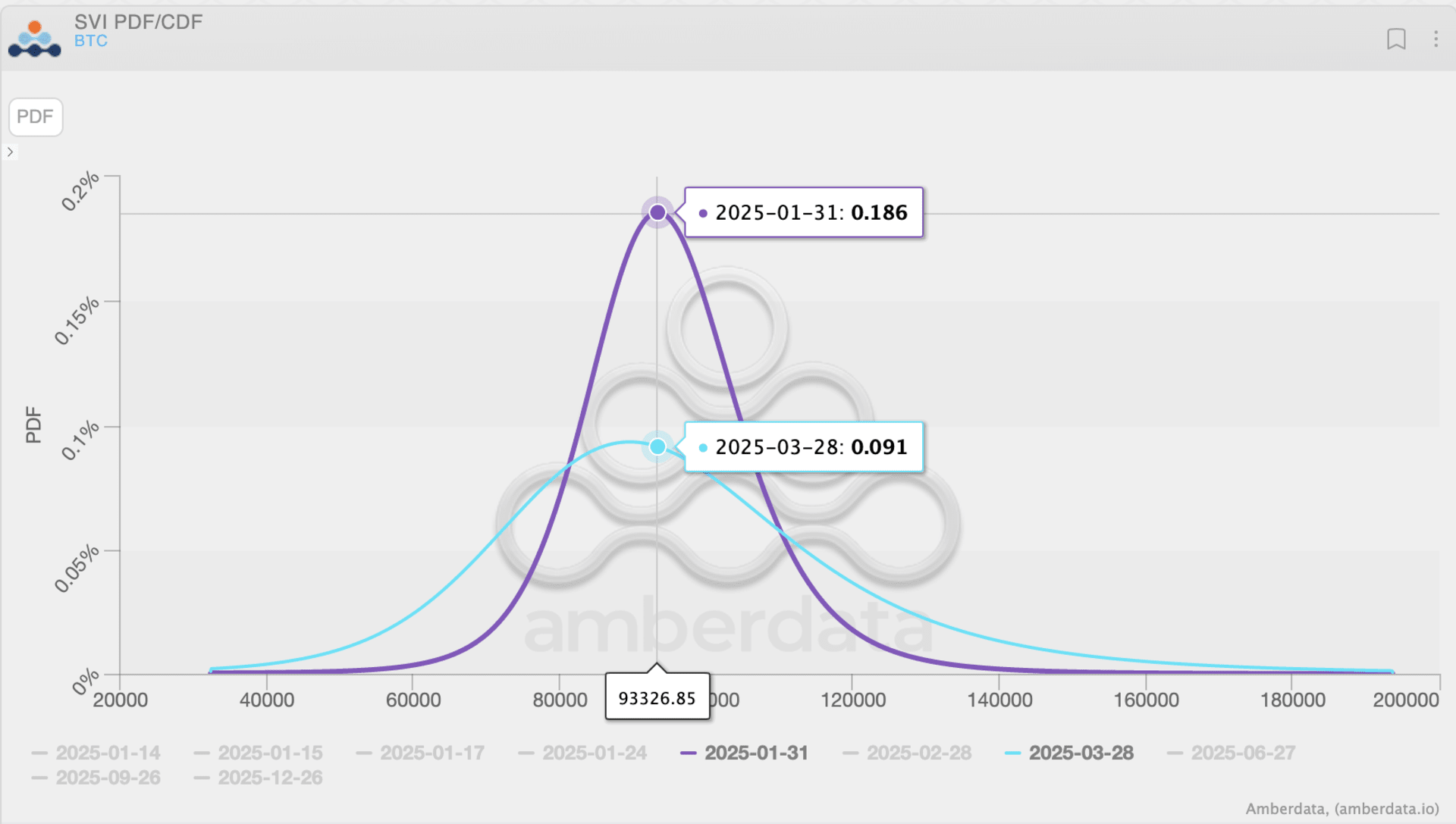
Amberdata 期权 PDF

Amberdata PDF 图表展示了比特币在不同日期到期时的概率密度函数（PDF）。以下是对该图表的解释和分析方法：

PDF（概率密度函数）：
- 纵轴：显示概率密度值。
- 横轴：显示比特币的价格。
- 不同颜色的曲线代表在不同日期到期时的价格分布。例如：
  - 紫色曲线代表 2025 年 1 月 31 日的到期日。
  - 蓝色曲线代表 2025 年 3 月 28 日的到期日。
峰值和分布：
- 每条曲线的峰值表示比特币在对应日期到期时的最可能价格范围。比如在 2025 年 1 月 31 日，峰值约为 0.186，表明在该价格附近的出现概率最高。
- 曲线的形状和分布可以反映市场对不同价格区间的预期概率。

识别峰值
- 找出每条 PDF 曲线的峰值，这代表比特币在特定到期日期的最有可能价格。例如，2025 年 1 月 31 日的峰值在约 93,326.85 美元。
比较不同到期日的分布
- 通过对比不同颜色曲线的分布，可以看到比特币价格在不同到期日的市场预期如何变化。例如，2025 年 3 月 28 日的分布相比 2025 年 1 月 31 日要更加平坦，表示市场认为价格更加分散，波动较大。
评估风险和机会
- 曲线的“厚尾”部分（尾部较长）表示有较低概率的极端价格变化。此特性对风险管理和期权定价非常重要，因为它反映市场对剧烈价格变动的预期。

Cumulative distribution function 翻译为累积分布函数，可以用来观测不同到期日价格超过某个行权价概率。

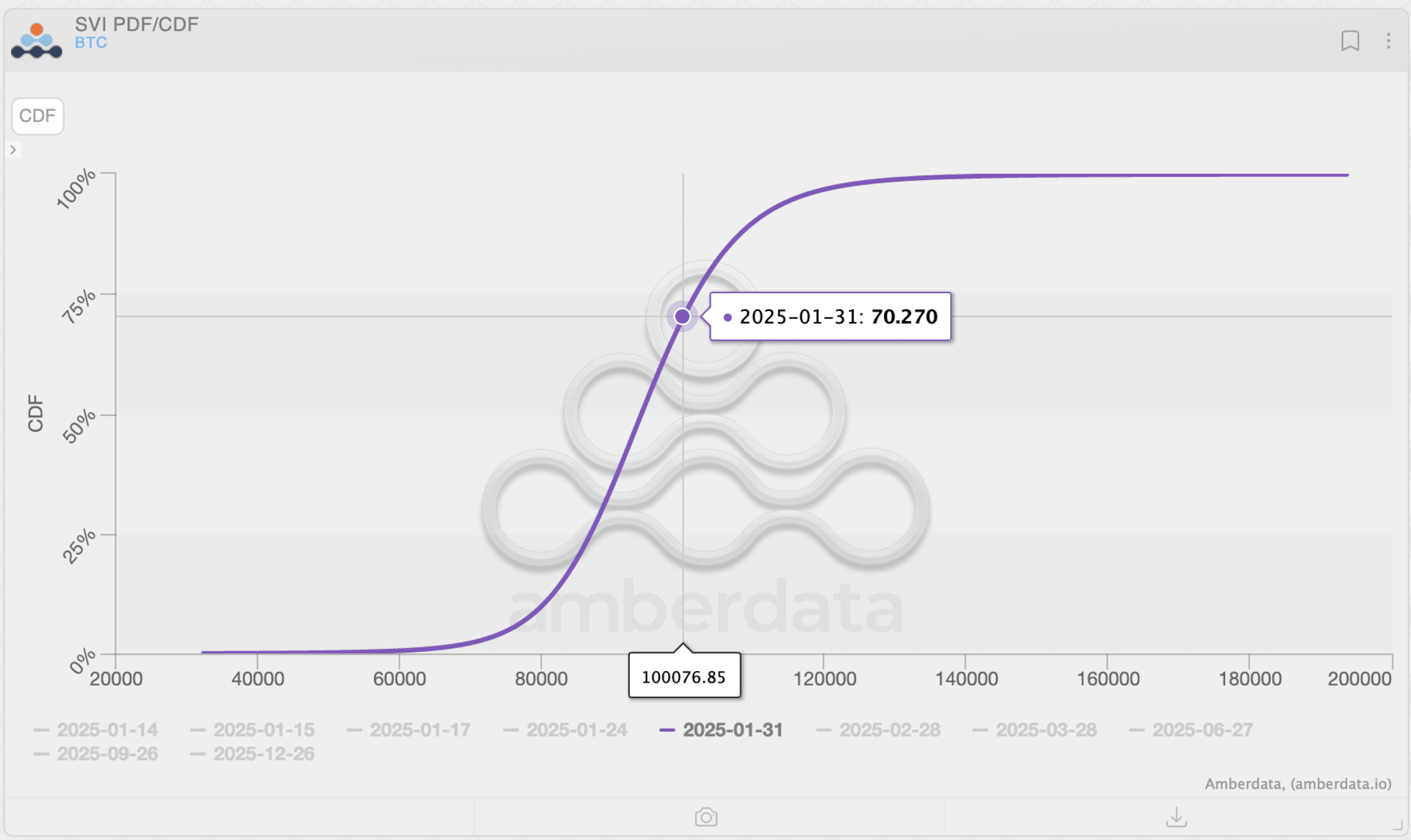
Amberdata 期权 CDF

Amberdata CDF 图表展示了比特币在不同价格水平上的累积概率分布函数（CDF）。以下是对该图表的解释和分析方法：

CDF（累积分布函数）：
- 纵轴：显示累积概率值，以百分比表示。
- 横轴：显示比特币的价格。
- 不同颜色的曲线代表在不同日期到期时的价格累积分布。例如：
  - 紫色曲线代表 2025 年 1 月 31 日的到期日。
关键点解读：
- 数值标签：箭头所指向的点代表在某个价格水平和到期日时的累积概率。例如，2025 年 1 月 31 日，比特币价格在 100,076.85 美元以上概率约为 (100-70.27)%。

识别累积概率
- 找出这些关键点，了解某个价格水平的累积概率。例如，2025 年 1 月 31 日，比特币价格达到或低于 100,076.85 美元的概率约为 70.27%。
确定概率区间
- 分析累计概率曲线的平滑程度和陡峭程度，以确定价格在特定区间的概率。例如，从图上可以看出，价格在 40,000 美元至 80,000 美元之间的累积概率增幅较慢，而在 80,000 美元至 120,000 美元之间增幅较快。
逆向求值
- 通过确定某个累积概率来反求价格水平。例如，如果想知道比特币价格超过 120,000 美元的概率，可以看到 CDF 在 120,000 美元附近趋近于平稳，此时累积概率接近 100%，可以计算出剩余概率很小。也即到期时超过 12 万的概率几乎为零